R语言与数据分析（三）

R语言数据分析

数据分析

发布日期: 2020-06-26

更新日期: 2023-09-10

阅读次数:

喜欢一件事就去争取吧。

48-相关性检验函数

在计算好相关性系数之后就可以进行统计学的显著性检验

需要量化才能证明两个系数的相关性

还是之前的例子,检测下文盲率和谋杀率之间的关系

> library(ggm)
> ?cor.test
> cor.test(state.x77[,3],state.x77[,5])

	Pearson's product-moment correlation

data:  state.x77[, 3] and state.x77[, 5]
t = 6.8479, df = 48, p-value = 1.258e-08  ## 这里是小于0.05的,说明相关
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:  ## 这是是置信区间,是统计学中重要的概念
 0.5279280 0.8207295
sample estimates:
      cor 
0.7029752  ## 这是是相关系数

置信区间

置信区间: confidence interval,是指由样本统计量所构造的总体参数的估计区间。在统计学中,一个概率样本的置信区间是对这个样本的某个总体参数的区间估计。置信区间展现的是这个参数的真实值有一定概率落在测量结果的周围的程度。置信区间给出的是被测量参数的测量值的可信程度。

简单的说就是,光给出概率不行,还得给出概率发生的范围.

psych 包中的 corr.test可以一次性计算多个变量之间的计算

> corr.test(state.x77)  ## 这里我的电脑加载不来

pcor.test 可用于偏相关的检验

> x = pcor(c(1,5,2,3,6),cov(state.x77))
## 参数依次为,偏相关系数,控制的变量数,样本数
## 2,3,6三个变量,总共50个州
> pcor.test(x,3,50)
$tval  ## 学生t检验统计
[1] 2.476049

$df  ## 自由度
[1] 45

$pvalue  ## p值
[1] 0.01711252

分组数据的相关性检验,差异发生的概率,从而比较两个平均数的差异是否显著,主要用于样本含量小,一般小于30个的,总体标准差未知的正太分布数据.

t检验

## 格式为 y~x,其中的y是一个数值型变量，x是一个二分型的变量
> ?t.test()
> library(MASS)
> t.test(Prob ~ So,data = UScrime)

	Welch Two Sample t-test

data:  Prob by So
t = -3.8954, df = 24.925, p-value = 0.0006506
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -0.03852569 -0.01187439
sample estimates:
mean in group 0 mean in group 1 
     0.03851265      0.06371269 
>

非参数检验方差未知

非参数检验,在总体方差未知或知道甚少的情况下,利用样本数据对总体分布形态等进行推断的方法。由于非参数检验方法在推断过程中不涉及有关总体分布的参数,因而得名为”非参数”检验

参数检验

参数检验,是在总体分布形式已知的情况下,对总体分布的参数如均值、方差等进行推断的方法。也就是数据分布已知比如满足正态分布。

49-绘图函数

R中四大作图函数

基础绘图函数（graphics）默认加载
lattice包
ggplot2包
grid包

基础绘图包

常用的函数

arrows 箭头函数
hist 直方图
stars 形状图
pie 饼图
polygon 多边形图

查看展示内容

> demo(graphics)

R基础绘图系统分高级绘图和低级绘图，高级绘图可以一步到位。

散点图：x和y两个坐标数据
直方图：因子
热力图：数据矩阵
要做到看到一个图形就能知道是用那个数据，那个函数做出来

> plot(women)

R中的S3系统指属性，泛型函数，方法

> methods(plot)
> methods(summary)

par函数

par可以对绘图函数进行设置

> plot(as.factor(mtcars$cyl),col = c("red","green","blue"))

50-自定义函数

编写函数就是为了减少重复代码的书写

在R中直接数据函数名，不输入括号就能直接看到源代码

函数名称

函数命名与功能相关
可以是字母和数字的组合，但必须是字母开头

一些编程知识

51-R数据分析实战

小麦产量案例
药物实验
社会科学，失业率，犯罪率，
量化投资产业
一些反面的教材

52-线性回归（一）

回归regression ,通常指那些用一个或多个预测变量,也称自变量或解释变量,来预测响应变量,也称为因变量、效标变量或结果变量的方法。

通过解释变量来预测响应变量

人话就是根据很多数据的规律，找到这个数据改在的地方，回归到它本来的地方，

回归案例

锻炼时间与消耗卡路里之间是什么关系?
是直线关系还是曲线关系?
卡路里消耗到某个点后,锻炼是否还有效果?
对年轻人和老人影响一致吗?
对男性和女性影响一致吗?
对肥胖的人和苗条的人影响一致吗?

回归分析类型

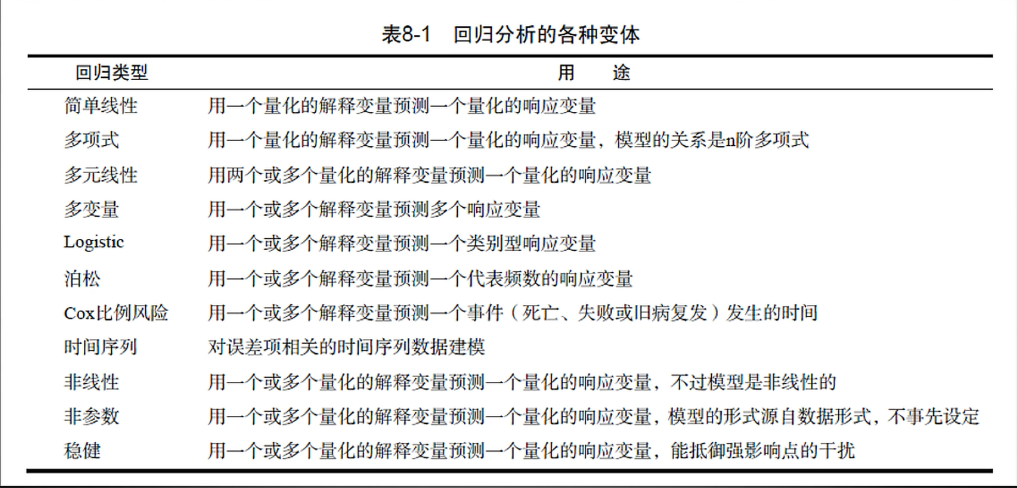
R表达式中常用的符号

普通最小而成回归法

> ?lm
> fit = lm(data = women,weight~height)
> fit

Call:
lm(formula = weight ~ height, data = women)

Coefficients:  ## 第一个为截距值，第二个是系数值
(Intercept)       height  
     -87.52         3.45 

> summary(fit)

Call:  ## 这里列出回归的公式
lm(formula = weight ~ height, data = women) 

Residuals:  ## 残差,真实值和预测值之间的差，如果残差全是0，那就是线性方程
    Min      1Q  Median      3Q     Max 
-1.7333 -1.1333 -0.3833  0.7417  3.1167 

Coefficients:  ## 系数项，intrecept为截距项，Estimate是系数
             Estimate Std. Error t value Pr(>|t|)   ## 这里的pr就是p值
(Intercept) -87.51667    5.93694  -14.74 1.71e-09 ***
height        3.45000    0.09114   37.85 1.09e-14 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.525 on 13 degrees of freedom
Multiple R-squared:  0.991,	Adjusted R-squared:  0.9903   ## 表示这个模型课程解释多少比例的数据
F-statistic:  1433 on 1 and 13 DF,  p-value: 1.091e-14  ## F统计量，p值来衡量，越小越好，越显著。大于0.05时不适用

53-线性回归（二）

线性回归常用函数

> plot(fit)

会生成四幅图,分别时残差拟合图,正太QQ图,大小位列图,残差影响图

> plot(women)
> abline(fit)  ## 这样就可以在原图上画出回归直线,abline只适用于直线

多项式回归,可以更好的拟合数据

注意公式,

至于什么时候加,要根据你自己对数据的理解不断尝试,

> fit2 = lm(data = women,weight~height+I(height^2))
> fit2
> summary(fit2)  ## 其中的解释更好
> plot(women)
> abline(fit)
## 第一个参数时横坐标的数值,第二个参数时根据拟合曲线得出的对应值
> lines(women$height,fitted(fit2),col = "red")

54-多元线性回归

当预测变量不止一个时，就变成了多元线性回归，相当于求解多元方程，难得时有些变量权重不一样，有些很大有些很小

> fir = lm(data = states,Murder ~ Population+Illiteracy+Income+Frost)
> summary(fir)
Call:
lm(formula = Murder ~ Population + Illiteracy + Income + Frost, 
    data = states)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.7960 -1.6495 -0.0811  1.4815  7.6210 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 1.235e+00  3.866e+00   0.319   0.7510    
Population  2.237e-04  9.052e-05   2.471   0.0173 *  
Illiteracy  4.143e+00  8.744e-01   4.738 2.19e-05 ***  ## 可以看到与文盲率相关性很大
Income      6.442e-05  6.837e-04   0.094   0.9253    
Frost       5.813e-04  1.005e-02   0.058   0.9541    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.535 on 45 degrees of freedom
Multiple R-squared:  0.567,	Adjusted R-squared:  0.5285 
F-statistic: 14.73 on 4 and 45 DF,  p-value: 9.133e-08

## 根据系数项和截距项就可以写出方程
> coef(fir)
 (Intercept)   Population   Illiteracy       Income        Frost 
1.2345634112 0.0002236754 4.1428365903 0.0000644247 0.0005813055

逐步回归

多个模型之间的关系,一次添加一个或者减少一个,直到模型不变

55-回归诊断

诊断要做的

这个模型是否是最佳模型？
模型多大程度满足OLS模型的统计假设?
模型是否经得起更多数据的检验?
如果拟合出来的模型指标不好,该如何继续下去?

满足OLS模型统计,只有满足这些条件才可以用lm函数进行拟合

正态性:对于固定的自变量值,因变量值成正态分布。
独立性:因变量之间相互独立。
线性:因变量与自变量之间为线性相关
同方差性:因变量的方差不随自变量的水平不同而变化。也可称作不变方差。

分别时残差拟合图,正太QQ图,大小位列图,残差影响图,查阅资料看下这些图的作用

> fit = lm(data = women, weight~height)
> par(mfrow=c(2,2))  ## 同时显示四幅图
> plot(fit)
## 出来的四幅图就是来评价这些条件的

抽样法验证

数据集中有1000个样本,随机抽取500个数据进行回归分析;
模型建好之后,利用predict函数,对剩余500个样本进行预测,比较残差值;श,接入入採人人
如果预测准确,说明模型可以,否则就需要调整模型。

56-方差分析(一)

方差分析,称为Analysis of Variance ,简称ANOVA,也称为“变异数分析” ,用于两个及两个以上样本均数差别的显著性检验。从广义上来讲,方差分析也属于回归分析的一种。只不过线性回归的因变量一般是连续型变量。而当自变量是因子时,研究关注的重点通常会从预测转向不同组之间差异的比较。这就是方差分析。

R中因子的应用

计算频数
独立性检验
相关性检验
方差分析
主成分分析
因子分析

方差分析的种类

单因素方差分析ANOVA (组内,组间)
双因素方差分析ANOVA
协方差分析ANCOVA
多元方差分析MANOVA
多元方差分析MANCOVA

顺序很重要

57-方差分析(二)

方差发案例,方差分析主要是看F值和P值

单因素方差分析

降低胆固醇药物的五种治疗方法的数据

没听懂,这里老师讲的莫名其妙的,可以查资料寻找方法

协方差分析

> ?litter
> attach(litter)
## 因变量werght,协变量gesttime,自变量dose
> fit3 = avo(weight ~ gesttime+dose,data = litter)
> summary(fit3)
            Df Sum Sq Mean Sq F value  Pr(>F)   
gesttime     1  134.3  134.30   8.049 0.00597 **  ## 怀孕时间,和体重
dose         3  137.1   45.71   2.739 0.04988 *   ## 计量与体重
Residuals   69 1151.3   16.69                   
---
Signif. codes:  
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

双因素分析案例

橙汁和维生素c的为食,60只豚鼠,牙齿的生长

> ?ToothGrowth
> attach(ToothGrowth)
> xtabs(~supp+dose)
    dose
supp 0.5  1  2
  OJ  10 10 10
  VC  10 10 10
> dose1 = factor(ToothGrowth$dose)  ## 讲dose转化为因子
> fit = aov(data = ToothGrowth,len~supp*dose1)
> summary(fit)
            Df Sum Sq Mean Sq F value   Pr(>F)    
supp         1  205.4   205.4  15.572 0.000231 ***  
## 说明为食方法对牙齿的生长有影响,
dose1        2 2426.4  1213.2  92.000  < 2e-16 ***
## 说明为食计量对牙齿的生长也有影响
supp:dose1   2  108.3    54.2   4.107 0.021860 *  
Residuals   54  712.1    13.2                     
---
Signif. codes:  
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

看不懂列的公式了,,,

58-功效分析

在这里条论下数据分析中应该使用多少的样本,如果样本少,p值小也是不可信.

在给定的置信度和概率下计算出所要的样本量,这就是功效分析了

功效分析, power analysis ,可以帮助在给定置信度的情况下,判断检测到给定效应值时所需的样本量。反过来,它也可以在给定置信度水平情况下,计算在某样本量内能检测到给定效应值的概率。

功效分析函数

功效分析理论基础

I型错误就是假阳性,II型错误就是假阴性

样本大小指的是实验设计中每种条件/组中观测的数目。
显著性水平(也称为alpha)由型错误的概率来定义。也可以把它看做是发现效应不发生的概率。
功效通过减去1型错误的概率来定义。我们可以把它看做是真实效应发生的概率。
效应值指的是在备择或研究假设下效应的量。效应值的表达式依赖于假设检验中使用的统计方法。

给出任意三种就可以推算第四种

线性回归功效的案例

假设显著性在0.05,那么在90%的置信度的情况下,需要多少的受试者才能得到这样方差

pwr包

pwr.f2.test,U为分子自由度,V为分母自由度,f2是效应值,sig.level为显著水平,power为功效水平

> library(pwr)
> pwr.f2.test(u=3,sig.level = 0.05,power = 0.9,f2 = 0.0769)

     Multiple regression power calculation 

              u = 3
              v = 184.2426
             f2 = 0.0769
      sig.level = 0.05
          power = 0.9

方差分析功效分析案例

一个单因素方差分析,要达到0.9的功效,效应值为0.25,0.05的显著水平,计算每组的样本量

pwr.anova.test 其中k为组的个数,n是各组的样本大小,也是要求的量,f是效应值

## 分两组,每组85个样本
> pwr.anova.test(k=2,f=0.25,sig.level = 0.05,power = 0.9)

     Balanced one-way analysis of variance power calculation 

              k = 2
              n = 85.03128
              f = 0.25
      sig.level = 0.05
          power = 0.9

NOTE: n is number in each group

59-广义线性模型

在自己应用中很多数据都是无规则分布的,要通过分析来找到规律

线性回归和方差分析都是基于正态分布的假设,广义线性模型扩展了线性模型的框架,它包含了非正态因变量的分析。

可以用glm进行广义线性回归分析,与lm类似

glm函数中重要的概率分布函数family,和相应的连接函数faction

广义线性的拟合

可用于的分布

binomial(link = “logit”) 二分项分布
gaussian(link = “identity”)
Gamma(link = “inverse”)
inverse.gaussian(link = “1/mu^2”)
poisson(link = “log”)
quasi(link = “identity”, variance = “constant”)
quasibinomial(link = “logit”)
quasipoisson(link = “log”)

泊松回归

泊松回归是用来为计数资料和列联表建模的一种回归分析。泊松回归假设因变量是泊松分布,并假设它平均值的对数可被未知参数的线性组合建模。

泊松分布可用于什么?

这里对一个癫痫病的年龄和发病率之间的数据

> ?glm
> data(breslow.dat,package = "robust")  ## 加载数据集
> attach(breslow.dat)  ## 获取这个数据集
> fit4 = glm(data = breslow.dat,family = poisson(link = "log",sumY~Base+Trt+Age))  ## sumY为因变量

> summary(fit4)

Call:
glm(formula = sumY ~ Base + Trt + Age, family = poisson(link = "log"), 
    data = breslow.dat)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-6.0569  -2.0433  -0.9397   0.7929  11.0061  

Coefficients:
               Estimate Std. Error z value Pr(>|z|)
(Intercept)   1.9488259  0.1356191  14.370  < 2e-16
Base          0.0226517  0.0005093  44.476  < 2e-16
Trtprogabide -0.1527009  0.0478051  -3.194   0.0014
Age           0.0227401  0.0040240   5.651 1.59e-08
                
(Intercept)  ***
Base         ***
Trtprogabide ** 
Age          ***
---
Signif. codes:  
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 2122.73  on 58  degrees of freedom
Residual deviance:  559.44  on 55  degrees of freedom
AIC: 850.71

Number of Fisher Scoring iterations: 5

> coef(fit4)  ## 显示个变量的系数,这里的截距没意义一
 (Intercept)         Base Trtprogabide          Age 
  1.94882593   0.02265174  -0.15270095   0.02274013 
> exp(coef(fit4))  ## 因为是对数,取指数才与因变量成正比
 (Intercept)         Base Trtprogabide          Age 
   7.0204403    1.0229102    0.8583864    1.0230007  ## 这里相等于年龄长一岁,期望的癫痫病发病率将乘以1.023

60-Logistic回归

当通过一系列连续型或类别型预测变量来预测二值型结果变量时Logistic回归是一个非常有用的工具。

logistic回归案例

根据危险因素预测某疾病发生的概率。例如,想探讨胃癌发生的危险因素,可以选择两组人群,一组是胃癌组,一组是非胃癌组,两组人群肯定有不同的体征和生活方式等。这里的因变量就是是否胃癌,即”是”或“否” ,为两分类变量,自变量就可以包括很多了,例如年龄、性别.饮食习惯、幽门螺杆菌感染等。自变量既可以是连续的,也可以是分类的。通过logistic回归分析,就可以大致了解到底哪些因素是胃癌的危险因素

出轨数据集

> ?Affairs
> data("Affairs",package = "AER")
> summary(Affairs)

老师操作猛如虎,,,看不懂

61-主成分分析

就是把很多不相干的数据去除,,降维处理

主成分分析

主成分分析, Principal Component Analysis,也简称为PCA,是一种数据降维技巧,它能将大量相关变量转化为一组很少的不相关变量,这些无关的变量称为主成分。主成分其实是对原始变量重新进行线性组合将原先众多具有一定相关性的指标,重新组合为一组的新的相互独立的综合指标。

相当于聚类,有联系的聚在一组,成为独立的一簇

相关性最大的为Pc1,第二的为a1x1,第三的为a2x2,,,a_k*X_k

R中自带的princomp可以进行主成分分析

> ?princomp
>

利用pshch中的

主成分分析与因子分析步骤

数据预处理;
选择分析模型;
判断要选择的主成分/因子数目; ## 通过绘制碎石图
选择主成分烟子;
旋转主成分/因子;
解释结果;
计算主成分或因子得分。这步也是可选的。

对USJudgeRationgs数据集的预测

数据不需要处理了
PCA分析

判断要选择的主成分数目

> library(psych)
> fa.parallel(USJudgeRatings,fa = "pc",n.iter = 100)

碎石图什么原理,可以取研究下平行分析法

我的包加载不出来,奇怪的很

> pc = principal(USJudgeRatings,nfactors = 1,rotate = "none",scores = FALSE)

theing

https://theing.gitee.io/2020/06/26/r-shu-ju-fen-xi/r-yu-yan-ru-men-yu-shu-ju-fen-xi-bi-ji-san/

本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 theing !

R语言数据分析

生物信息学知识

喜欢一件事就去做吧，看看究竟是什么，未完待更。

2020-06-29 其他

生物信息

R语言与数据分析（二）

喜欢一件事就去争取吧。

2020-06-26 数据分析

R语言数据分析

R语言与数据分析（三）

48-相关性检验函数

置信区间

t检验

非参数检验 方差未知

参数检验

49-绘图函数

基础绘图包

par函数

50-自定义函数

函数名称

51-R数据分析实战

52-线性回归（一）

回归案例

回归分析类型

R表达式中常用的符号

普通最小而成回归法

53-线性回归（二）

多项式回归,可以更好的拟合数据

54-多元线性回归

逐步回归

55-回归诊断

满足OLS模型统计,只有满足这些条件才可以用lm函数进行拟合

抽样法验证

56-方差分析(一)

R中因子的应用

方差分析的种类

顺序很重要

57-方差分析(二)

单因素方差分析

协方差分析

双因素分析案例

58-功效分析

功效分析函数

功效分析理论基础

给出任意三种就可以推算第四种

线性回归功效的案例

pwr包

方差分析功效分析案例

59-广义线性模型

泊松回归

60-Logistic回归

logistic回归案例

61-主成分分析

主成分分析

R中自带的princomp可以进行主成分分析

利用pshch中的

主成分分析与因子分析步骤

对USJudgeRationgs数据集的预测

非参数检验方差未知